Resizmple
The past few months I've been doing research on Richard Miller's port of Plan9 for the Raspberry Pi4 with the intention of writing my senior thesis about my work. I think it's mentioned in my Experience or Projects section, but I also haven't updated either of those in a moment.
Recently, I was in the class I TA for. My students were quietly working on their assignment. It was 9am, so the other TA and I were exhausted, running on nothing but coffee and Monster energy drinks. We were making jokes about putting the iconic Windows XP background on things that definitely should not have the Windows XP background. I mentioned it would be funny to put it on Plan9 as a way of bothering the professor we TA for and my research advisor, Dr. Stuart. When I got home from lab, instead of working on my research like a good student, I sat down and decided to see how viable my joke would be.
Rio is the windowing system for Plan9. It normally does not support wallpapers. It typically has a plain gray background (#777777, to be exact). After a quick Google search, I was able to find an implementation for a wallpaper by Devine Lu Linvega. After a little fiddling, I was able to create the following image, which I emailed over to my research advisor.
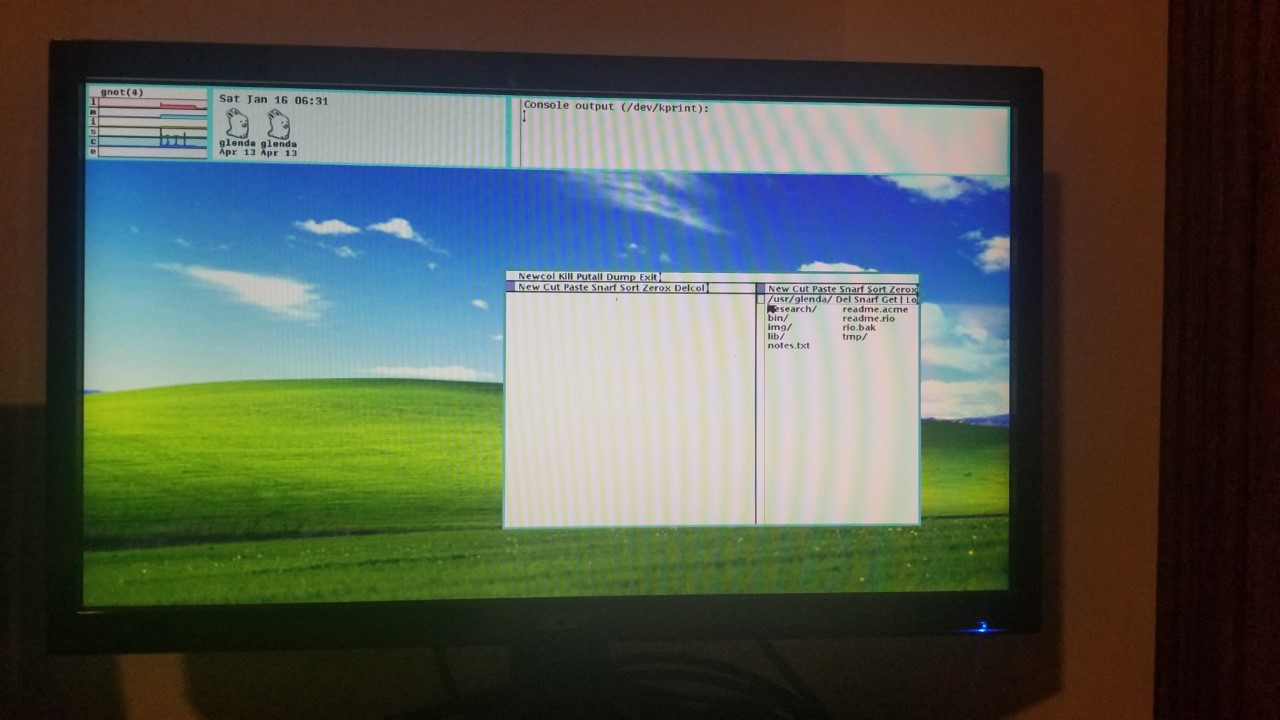
This earned me a quick 11pm "Uh huh" email. The next morning I got a second response, "Wait, did you actually modify rio to support wallpapers or is that image modified?" I gave Devine the credit they deserve, but mentioned I've got more plans for the wallpaper. Devine's implementation relys on the image already being the size of the window. If it's too small, it gets tiled. If it's too large, it gets cut off. Resizing the window only increases the tiling. I decided to take it upon myself to implement this functionality myself. As far as I'm aware, no one has done this for Plan9 yet.
I originally used the resample function to resize the image based on the dimensions of my monitor. A similar function didn't exist in C. So I took the time to learn the Plan9 Image format and wrote my own. I'm quite proud of how elegant the function turned out, so this blogpost is a tribute to it and the hours I poured into a whiteboard. I'll post the rest of the wallpaper implementation in about a week when I finish cleaning up other parts of the code.
I didn't know the
difference between resampling and resizing an image
at first, so I called my function resizmple as a joke while testing. The name
has grown on me now and I can't imagine changing it.
1 : fun resizmple(io, xo, yo, in, xn, yn, d) 2 : // Decide and calculate scalars xs and ys 3 : 4 : ro := 0 5 : for rn := 0 to yn do 6 : if yn > yo then 7 : if (rn * yo) > (ro * yn) then 8 : ro++ 9 : else 10 : if (rn * yo) < (ro * yn) then 11 : ro++ 12 : fi 13 : 14 : co := 0 15 : for cn := 0 to xn do 16 : if xn > xo then 17 : if (cn * xo) > (co * xn) then 18 : co++ 19 : else 20 : if (cn * xo) < (co * xn) then 21 : co++ 22 : fi 23 : 24 : po := ((ro * xo) + co) * d 25 : pn := ((rn * xn) + cn) * d 26 : 27 : for i := 0 to d do 28 : in[pn + i] := io[po + i] 29 : rof 30 : 31 : if xo > xn then 32 : co += xs 33 : rof 34 : 35 : if yo > yn then 36 : ro += ys 37 : rof 38 : end resizmple
Resizmple V1
I've taken enough Data Structures and Algorithms courses to know that it's
important to have a solid foundation on how you'll store your data before you
try writing an algorithm for it. I know the uncompressed Plan9 image format that
I would be working with gives me w * h pixels, each represented by d bytes.
I've got two main options for storing this data:
-
A simple array of length
w * h * dthat matches how the image data is actually stored-
The index of pixel
pat location(c, r)is referenced with((r * w) + c) * d)
-
The index of pixel
-
A three dimensional array that simulates the images output
-
An outermost array of length
h -
It's subarrays represent each row and have length
w -
It's subarrays represent each pixel and have length
d -
The index of pixel
pat location(c, r)is referenced withi[r][c]
-
An outermost array of length
While the second option appears more "intuitive", its over complicating the problem and the way the memory is being handled. I decided I can handle a simple math problem if it means I don't have to play with pointers. This brings me to my two major design principles I refused to waiver on:
- The images are represented through one dimensional arrays
- No fractional numbers
The fractional numbers just aren't worth the effort. This is meant to be a joke
project. I don't want to fight the intricacies of floating point numbers for a
silly background image. I use integer division to find our scalar xs. If we're
getting bigger, xs = ceil(xn/xo). If we're getting smaller, xs = ceil(xo/xn)
If we're getting smaller, the new image will take every xsth pixel from the
old image:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| a | b | c | d |
| 0 | 1 | 2 | 3 |
|---|---|---|---|
| a | b | c | d |
If we're getting bigger, each pixel in the old image will be duplicated xs
times:
| 0 | 1 | 2 | 3 |
|---|---|---|---|
| a | b | c | d |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| a | a | b | b | c | c | d | d |
This doesn't create the prettiest output. Decreasing the size of the image is lossy. Increasing the size of the image will create a blocky image. It's a small price to pay for Plan9XP. I'm not a computer vision or graphics manipulation person. I'm not going to write a resizing function based on color and eyes and behavior and stuff. I just want my silly joke to work.
The reason I avoid software engineering at all costs is that the user exists and interacts with my code. Typically I try to avoid writing code where the user has options, but I think tiled wallpapers are hideous in every situation, so I gave the user can specify how the image is scaled.
The image is not keeping the same dimensions
-
xandyare being scaled independently and have separatexsandysscalars
The image is keeping the same dimensions
-
The image is being scaled by
xs-
yn := yo * xs -
ys := xs
-
-
The image is being scaled by
ys-
xn := xo * ys -
xs := ys
-
-
The image is not being scaled, and will be tiled across the screen
-
xs = ys = 1 -
xn := xo -
yn := yo
-
In addition to this, going back to my core design principles, I want everything
done with integer values. So xs and ys must be whole numbers. I need to
independently handle the cases where xn > xo, xo > xn, yn > yo, and
yo > yn. Depending on the orginal size of the image and the size of the
window, these can be used in a variety of combinations with the above. I refuse
to write 30 different loops for each combination. I want to write one general
loop that can apply universally. Knowing that every single pixel in the new
image needs to be filled, I get the following starting structure for my loop:
1 : for rn := 0 to yn do 2 : for cn := 0 to xn do 3 : pn := ((rn * xn) + cn) * d 4 : po := ((ro * xo) + co) * d 5 : 6 : for i := 0 to d do 7 : in[pn + i] = io[po + i] 8 : rof 9 : rof 10 : rof
The next task is to decide which pixel po at location (co, ro) gets selected
from the old image io to be copied over to the new image in.
One of the benefits of the way I'm choosing pixels is that the rows and columns
are taken independently. The column being grabbed has no impact on the row being
grabbed and vice versa. So for the remainder of the explanation, I'm going to
focus on the x component only, since I know its concepts will apply to the y
component too. I'm also going to ignore the depth of the image for the time
being, since it has no affect on the pixel selection.
The image getting larger is easy because co is just cn * xs:
1 : for cn := 0 to xn do 2 : if xo > xn then 3 : co = cn * xs 4 : rof
Getting smaller isn't as easy because xo is now smaller than xn, meaning
co is smaller than cn and cannot equal cn * xs. We would instead get that
co = floor(cn / xs) which is using fractional numbers, which I don't want to
do.
Thinking about the rows and columns through a multiplication perspective won't
work. Knowing that multiplication is just repeated addition and a loop is
equivalent to a summation, then as cn increases by 1 each iteration, then
co increases by xs.
How does co increase when the image is getting smaller though? Pixels in the
old image are repeated in the new image. This means as cn increments by 1 each
iteration, co only increments by 1 every xsth iteration. I can adjust my
function accordingly:
1 : co = 0 2 : for cn := 0 to xn do 3 : if xo > xn then 4 : co += xs 5 : else if (xn > xo) and (cn % xs == 0) then 6 : co++ 7 : fi 8 : rof
Then this works and does what I wanted. Then I apply it to the full resizmple
function. Note that in practice, the scalars are calculated and decided based on
a config file the user writes.
1 : fun resizmple(io, xo, yo, in, xn, yn, d) 2 : // Decide and calculate scalars xs ys 3 : 4 : ro := 0 5 : for rn := 0 to yn do 6 : co := 0 7 : for cn := 0 to xn do 8 : po := ((ro * xo) + co) * d 9 : pn := ((rn * xn) + cn) * d 10 : 11 : for i := 0 to d do 12 : in[pn + i] := io[po + i] 13 : rof 14 : 15 : if xo > xn then 16 : co += xs 17 : else if (xn > xo) and (cn % xs == 0) then 18 : co++ 19 : fi 20 : rof 21 : 22 : if yo > yn then 23 : ro += ys 24 : else if (yn > yo) and (rn % ys == 0) then 25 : ro++ 26 : fi 27 : rof 28 : end resizmple
I wasn't exactly thrilled with this solution. While I knew I wasn't entirely
serious about this and didn't need the most robust scaling system, this was
borderline nonfunctional. I could only scale by values 1/n or n/1. Given
xo = 6 and xn = 9 then xs = ceil(xn / xo) = 2. So the image would double
in size, then get cut off. I had other fish to fry, so rewriting resizmple
would have to wait.
Resizmple V2
When I did get around to rewriting resizmple to support
non-integer scale values, I didn't want to actually use floats in my
algorithm. I was very happy with how my algorithm relied only on addition to
calculate the rows and columns and had no intention of changing this. I knew the
behavior I wanted to mimic, but I didn't know how to implement it. Given
xo := 13 and xn := 5, I wanted something like:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e |
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| a | b | c | d | e |
Here, the value I increase co by is not constant. I'm still losing xo - xn
columns of pixels in the compression, and that where I grabbed those columns
wouldn't matter too much, but I cared more about rewriting my algorithm to
handle scaling better. The biggest challenge would be calculating when I skip an
extra column. To get a better idea, I decided to look at how this would be
affected if I floored fractional numbers:
xo / xn = 13 / 5 = 2.2 c0 = floor(cn * 2.2)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e |
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| a | b | c | d | e |
I figured there has to be a way to do this using the modulo. So I made a few more tables trying to figure out how to incorporate a modulo:
xo / xn = v / 5 c0 = floor(cn * (v/5))
| 5 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 2 | 2 | 2 |
| 2 | 4 | 4 | 5 | 5 |
| 3 | 6 | 7 | 7 | 8 |
| 4 | 8 | 9 | 10 | 11 |
How much was co increased by?
| 5 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|
| 0 | ||||
| 1 | 2 | 2 | 2 | 2 |
| 2 | 2 | 2 | 3 | 3 |
| 3 | 2 | 3 | 2 | 3 |
| 4 | 2 | 2 | 3 | 3 |
When was co extra increased?
| 11 | 12 | 13 | 14 |
|---|---|---|---|
| 3 * (2/5) | 2 * (3/5) | 2 * (4/5) | |
| 4 * (3/5) | 3 * (4/5) | ||
| 4 * (4/5) | |||
| 11 | 12 | 13 | 14 |
| 6/5 | 6/5 | 8/5 | |
| 12/5 | 12/5 | ||
| 16/5 |
From this I realized that I've figured it out, and ended up with:
1 : xd := xo / xn 2 : xm := xo % xn 3 : xmi := 0 4 : 5 : co += xd 6 : if (cn * xm) > (xm * xmi ) then 7 : co++ 8 : xmi++ 9 : fi
Now what if we're getting larger?
cn = floor((xn / xo) * co)
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| a | b | c | d | e |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | a | b | b | b | c | c | d | d | d | e | e | e |
This technically works, but co is our unknown, and we can't take it out of the
floor. If we took it out and only floored the division step, then we'd lose
the non integer scale value I've been trying to hold onto. Looking at how many
extra variables I had to add for getting smaller and then the problem in front
of me, I was about to give up and use floats when I realized:
cn xn -- = -- co xo
It's just a ratio. I wrote the explanation for V2 before V1, so in writing how
I wrote V1, I'm kicking myself a lot for not recognizing this earlier.
We already know the scale is xn/xo. If cn is consistently
increasing, then we need to increase co when this ratio doesn't hold anymore.
This gives:
cn * xo = co * xn
When we're getting bigger and xn > xo then the ratio "breaks" when
cn * xo > co * xn. Now we need to increase co. This ensures we grab many
co for each cn. Then when getting smaller and xo > xn then the ratio
"breaks" when cn * xo < co * xn. The key here is that co is already
increasing by the integer division xo/xn each turn, so it has to remain
"further along" than cn. Instead of that ugly modulus mess above, I now can
apply this concept to both the x and y components and get my resizmple
algorithm with no division!
1 : fun resizmple(io, xo, yo, in, xn, yn, d) 2 : // Decide and calculate scalars xs and ys 3 : 4 : ro := 0 5 : for rn := 0 to yn do 6 : if yn > yo then 7 : if (rn * yo) > (ro * yn) then 8 : ro++ 9 : else 10 : if (rn * yo) < (ro * yn) then 11 : ro++ 12 : fi 13 : 14 : co := 0 15 : for cn := 0 to xn do 16 : if xn > xo then 17 : if (cn * xo) > (co * xn) then 18 : co++ 19 : else 20 : if (cn * xo) < (co * xn) then 21 : co++ 22 : fi 23 : 24 : po := ((ro * xo) + co) * d 25 : pn := ((rn * xn) + cn) * d 26 : 27 : for i := 0 to d do 28 : in[pn] := io[po] 29 : rof 30 : 31 : if xo > xn then 32 : co += xs 33 : rof 34 : 35 : if yo > yn then 36 : ro += ys 37 : rof 38 : end resizmple
While the scalars appear to be calculated through division and flooring, it's
not necessary. For a dimension d, the scalar ds between two values where
d1 > d0 is calculated with:
1 : for( ds := 0; ds * d0 < d1; ds++ )
Overall, I'm very proud of my little solution. My advisor related it to Bresenham's Line Drawing Algorithm in how Bresenham probably figured out his solution. He told me to write down my solution. I'm glad I did. It was fun to break it down and reinforce why it works. I also took the time to do a bit of reformatting on the site and wrote a syntax highlighter for psuedo code. Those are separate blogposts though. I've
Back to Top